Code Refactoring#
Code refactoring is the process of restructuring existing computer code—changing the factoring—without changing its external behavior. (Wikipedia)
When tackling a problem you will often not have an idea, initially, of what you’re really doing.
This lack of understanding will be reflected in the code that you write to solve the problem.
Refactoring a piece of code after an initial implementation (and after verifying, with tests, that it works) has 2 benefits:
Looking critically at the code can help you understand the problem better
When you have a better understanding of the problem, your code can better reflect the structure of the problem. This will usually make it easier to read.
As a concrete example let’s take the exercise on if/else from day 1.
If, if, if, ….#
In this exercise you will be making geometric pictures using if-clauses. To this end you will program a python function f(x, y) that takes inputs x and y ranging from 0 to 10, and that returns a number from 0 to 5. This function can then be plotted in a color plot.
The color plot we have prepared for you in a helper function (you will learn in day 2 about how to plot things in python):
from helpers import plot_function
As an example, let’s make a function that returns one value if x < 5, and another for x >= 5:
def f(x, y):
if x < 5:
return 1
else:
return 4
We can now use the helper plot_function to represent our function f(x, y) as a color plot:
plot_function(f)
Write your own f(x, y) to reproduce pictures like the ones given below
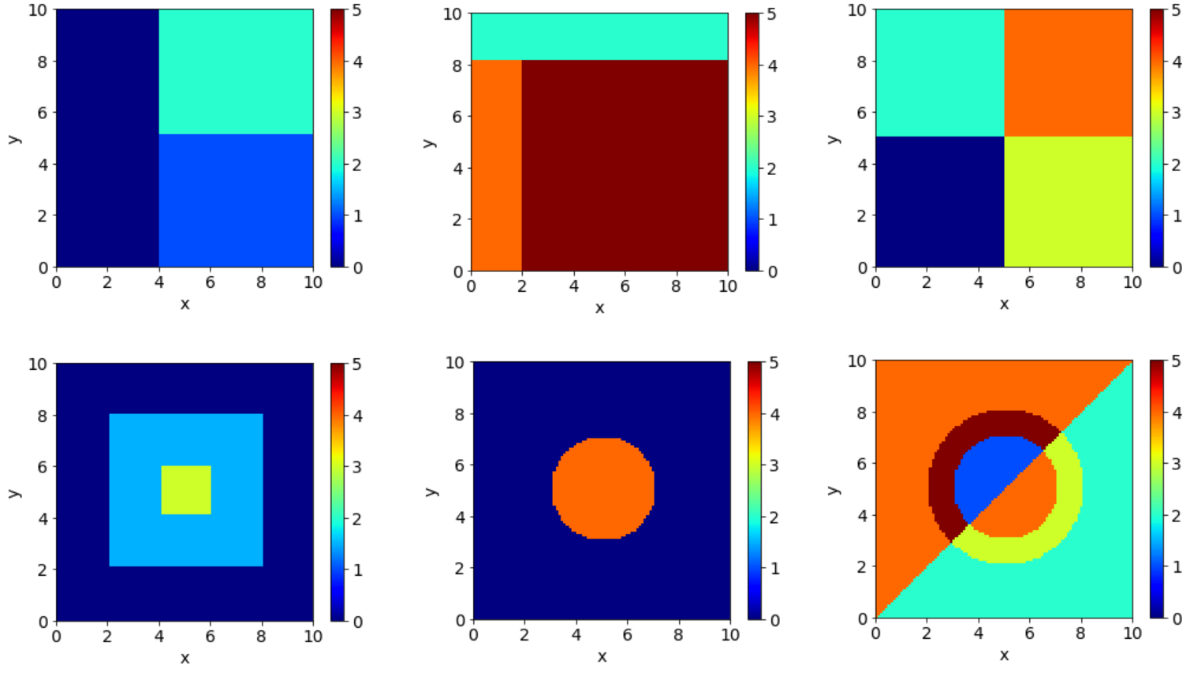
For the moment let’s take the most complex example on the lower right.
from math import sqrt
def f(x, y):
if x < y:
if sqrt((x - 5)**2 + (y - 5)**2) >= 2 and sqrt((x - 5)**2 + (y - 5)**2) < 3:
return 5
elif sqrt((x - 5)**2 + (y - 5)**2) < 2:
return 1
else:
return 4
else:
if sqrt((x - 5)**2 + (y - 5)**2) >= 2 and sqrt((x - 5)**2 + (y - 5)**2) < 3:
return 3
elif sqrt((x - 5)**2 + (y - 5)**2) < 2:
return 4
else:
return 2
plot_function(f)
Why is this code good?#
It works!
Why is this code bad?#
It doesn’t have any tests
It’s not clear why it works
We recalculate the same thing several times
Golden rule of refactoring#
When your code works, before you touch anything, make sure you have comprehensive tests. Without tests, you won’t know when you break something
def test_f():
assert f(1, 0) == 2
assert f(0, 1) == 4
assert f(5, 4) == 4
assert f(4, 5) == 1
assert f(5, 2.5) == 3
assert f(2.5, 5) == 5
test_f()
Note that in this specific example where we generate an image the best test is probably just to display the image!
Let’s have another go, avoiding repeating ourselves.
# Changes
# + define r_center
# + re-order if-s to make the conditions simpler
from math import sqrt
def f(x, y):
r_center = sqrt((x - 5)**2 + (y - 5)**2)
if x < y:
if r_center < 2:
return 1
elif r_center < 3:
return 5
else:
return 4
else:
if r_center < 2:
return 4
elif r_center < 3:
return 3
else:
return 2
def test_f():
assert f(1, 0) == 2
assert f(0, 1) == 4
assert f(5, 4) == 4
assert f(4, 5) == 1
assert f(5, 2.5) == 3
assert f(2.5, 5) == 5
test_f()
plot_function(f)
This is much better, but it’s still quite complicated. We see that there’s this if-else chain that has the same structure:
if r_center < 2:
return <something>
elif r_center < 3:
return <something else>
else:
return <another thing>
How can we make this better?
# Changes
# + define r_center
# + re-order if-s to make the conditions simpler
# + factor out inner condition into a separate function
from math import sqrt
def inner_condition(r_center, values):
if r_center < 2:
return values[0]
elif r_center < 3:
return values[1]
else:
return values[2]
def f(x, y):
r_center = sqrt((x - 5)**2 + (y - 5)**2)
if x < y:
values = [1, 5, 4]
else:
values = [4, 3, 2]
return inner_condition(r_center, values)
def test_f():
assert f(1, 0) == 2
assert f(0, 1) == 4
assert f(5, 4) == 4
assert f(4, 5) == 1
assert f(5, 2.5) == 3
assert f(2.5, 5) == 5
test_f()
plot_function(f)
Question#
Is the code better or worse?
Answer#
Arguably, it’s worse.
Even though we’ve factored out the inner conditionals into a separate function (code re-use!), the code is now harder to understand.
It’s harder to understand because the function inner_condition does not really correspond to a useful concept in the problem space.
Identifying the structure of the problem#
Let’s step back for a minute and take another look at the original problem.
We need to construct functions that correspond to each of these images. What do we notice about each of these images? They’re constructed from regular shapes, not random blobs! Each of the pictures can be decomposed into a combination of simpler shapes.
Perhaps if we use the “shape” concept we can make our code even better.

Taking the lower-right example again, we notice 2 types of shape:
circles with different radiuses
diagonal lines bisecting the plane
Let’s make these into concepts in the code. We’ll make 2 functions that tell us if a point is in a circle, or in the upper-diagonal of the plane:
def in_circle(x, y, center, radius):
return (x - center)**2 + (y - center)**2 < radius**2
def in_upper_diagonal(x, y):
return x < y
Now we can use these functions within our f:
from math import sqrt
def f(x, y):
if in_circle(x, y, center=5, radius=2):
return (1 if in_upper_diagonal(x, y) else 4)
elif in_circle(x, y, center=5, radius=3):
return (5 if in_upper_diagonal(x, y) else 3)
else:
return (4 if in_upper_diagonal(x, y) else 2)
def test_f():
assert f(1, 0) == 2
assert f(0, 1) == 4
assert f(5, 4) == 4
assert f(4, 5) == 1
assert f(5, 2.5) == 3
assert f(2.5, 5) == 5
test_f()
plot_function(f)
You may argue that this approximately as readable as the previous example, however the fact that we’ve identified the correct problem decomposition is useful because it provides us with a framework to tackle all the other problems in the same class:
def plane_with_circle(x, y):
return 4 if in_circle(x, y, center=5, radius=2) else 0
plot_function(plane_with_circle)
def in_square(x, y, center, length):
lower = center - length / 2
upper = center + length / 2
return (lower < x < upper) and (lower < y < upper)
def concentric_squares(x, y):
if in_square(x, y, center=5, length=2):
return 3
elif in_square(x, y, center=5, length=6):
return 2
else:
return 0
plot_function(concentric_squares)